Баллистика корабельной артиллерии
| Версия 12:58, 31 октября 2014 zxmerlin:ru переименовал страницу Стрельба корабельной артиллерии в Navy:Баллистика корабельной артиллерии | Версия 07:20, 2 ноября 2014 | |||
| Строка 1: | Строка 1: | |||
| ? | [[Файл:Ship Gun.jpg|400 px|thumbnail|Артиллерия линейного корабля "Марат"]] | + | [[Файл:Ship Gun.jpg|400 px|thumbnail|Рис. 1. Артиллерия линейного корабля "Марат"]] | |
| {{AnnoWiki | {{AnnoWiki | |||
| |content = '''Корабе́льная артилле́рия''' — совокупность артиллерийского оружия, установленного на боевых кораблях и предназначенного для применения по береговым (наземным), морским (надводным) и воздушным целям.}} | |content = '''Корабе́льная артилле́рия''' — совокупность артиллерийского оружия, установленного на боевых кораблях и предназначенного для применения по береговым (наземным), морским (надводным) и воздушным целям.}} | |||
| Строка 5: | Строка 5: | |||
| == Основные понятия == | == Основные понятия == | |||
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca27.png|400 px|thumb|right|Элементы стрельбы корабельной артиллерии]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca27.png|400 px|thumb|right|Рис. 2. Элементы стрельбы корабельной артиллерии]] | |
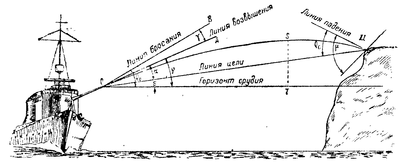
| '''''Точкой вылета''''' называется центр дульного среза орудия.<br /> | '''''Точкой вылета''''' называется центр дульного среза орудия.<br /> | |||
| Строка 14: | Строка 14: | |||
| '''''Линией возвышения''''' называется продолжение оси канала ствола наведённого орудия.<br /> | '''''Линией возвышения''''' называется продолжение оси канала ствола наведённого орудия.<br /> | |||
| ? | '''''Линией бросания''''' ОВ называется продолжение оси канала ствола в момент выстрела. В момент выстрела орудие вздрагивает, вследствие чего снаряд бросается не по линии возвышения ОА, а по линии бросания ОВ.<br /> | + | '''''Линией бросания''''' ОВ называется продолжение оси канала ствола в момент выстрела. В момент выстрела орудие вздрагивает, вследствие чего снаряд бросается не по линии возвышения ОА, а по линии бросания ОВ (см. рис. 2).<br /> | |
| ? | '''''Линией цели''''' ОЦ называется линия, соединяющая орудие с целью.<br /> | + | '''''Линией цели''''' ОЦ называется линия, соединяющая орудие с целью (см. рис. 2).<br /> | |
| '''''Линией прицеливания (визирования)''''' называется линия, идущая от глаза наводчика через оптическую ось прицела в точку наводки. При стрельбе прямой наводкой, когда линия прицеливания направлена в цель, линия прицеливания совпадает с линией цели.<br /> | '''''Линией прицеливания (визирования)''''' называется линия, идущая от глаза наводчика через оптическую ось прицела в точку наводки. При стрельбе прямой наводкой, когда линия прицеливания направлена в цель, линия прицеливания совпадает с линией цели.<br /> | |||
| '''''Линией падения''''' называется касательная к траектории в точке падения. | '''''Линией падения''''' называется касательная к траектории в точке падения. | |||
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca28.png|400 px|thumb|right|Стрельба по вышележащей цели]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca28.png|400 px|thumb|right|Рис. 3. Стрельба по вышележащей цели]] | |
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca29.png|400 px|thumb|right|Стрельба по нижележащей цели]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca29.png|400 px|thumb|right|Рис. 4. Стрельба по нижележащей цели]] | |
| ? | '''''Углом возвышения (греческая фи)''''' называется угол между линией возвышения и горизонтом орудия. Если ось канала ствола направлена ниже горизонта, то этот угол называется углом снижения.<br /> | + | '''''Углом возвышения (греческая фи)''''' называется угол между линией возвышения и горизонтом орудия. Если ось канала ствола направлена ниже горизонта, то этот угол называется углом снижения (см. рис. 2).<br /> | |
| ? | '''''Углом бросания (греческая тета ноль)''''' называется угол между линией бросания и горизонтом орудия.<br /> | + | '''''Углом бросания (греческая тета ноль)''''' называется угол между линией бросания и горизонтом орудия (см. рис. 2).<br /> | |
| ? | '''''Углом вылета (греческая гамма)''''' называется угол между линией бросания и линией возвышения. В морской артиллерии угол вылета имеет малую величину и его иногда в расчёт не принимают, полагая, что снаряд бросается под углом возвышения.<br /> | + | '''''Углом вылета (греческая гамма)''''' называется угол между линией бросания и линией возвышения. В морской артиллерии угол вылета имеет малую величину и его иногда в расчёт не принимают, полагая, что снаряд бросается под углом возвышения (см. рис. 2).<br /> | |
| ? | '''''Углом прицеливания (греческая альфа)''''' называется угол между линией возвышения и линией прицеливания.<br /> | + | '''''Углом прицеливания (греческая альфа)''''' называется угол между линией возвышения и линией прицеливания (см. рис. 2).<br /> | |
| ? | '''''Углом места цели (греческая эпсилон)''''' называется угол между линией цели и горизонтом орудия. При стрельбе корабля по морским целям угол места цели равен нулю, так как линия цели направлена по горизонту орудия.<br /> | + | '''''Углом места цели (греческая эпсилон)''''' называется угол между линией цели и горизонтом орудия. При стрельбе корабля по морским целям угол места цели равен нулю, так как линия цели направлена по горизонту орудия (см. рис. 2).<br /> | |
| ? | '''''Углом падения (греческая тета с латинской буквой с)''''' называется угол между линией цели и линией падения.<br /> | + | '''''Углом падения (греческая тета с латинской буквой с)''''' называется угол между линией цели и линией падения (см. рис. 2).<br /> | |
| ? | '''''Углом встречи (греческая мю)''''' называется угол между линией падения и касательной к поверхности цели в точке встречи.<br /> | + | '''''Углом встречи (греческая мю)''''' называется угол между линией падения и касательной к поверхности цели в точке встречи (см. рис. 2).<br /> | |
| '''''Плоскостью стрельбы''''' называется вертикальная плоскость, проходящая через линию возвышения. | '''''Плоскостью стрельбы''''' называется вертикальная плоскость, проходящая через линию возвышения. | |||
| При стрельбе корабля по морским целям линия прицеливания направлена по горизонту, в этом случае угол возвышения равен углу прицеливания. | При стрельбе корабля по морским целям линия прицеливания направлена по горизонту, в этом случае угол возвышения равен углу прицеливания. | |||
| ? | При стрельбе корабля по береговым и воздушным целям угол возвышения равен сумме угла прицеливания и угла места цели. | + | При стрельбе корабля по береговым и воздушным целям угол возвышения равен сумме угла прицеливания и угла места цели (см. рис. 3). | |
| ? | При стрельбе береговой батареи по морским целям угол возвышения равен разности угла прицеливания и угла места цели. | + | При стрельбе береговой батареи по морским целям угол возвышения равен разности угла прицеливания и угла места цели (см. рис. 4). | |
| + | Таким образом, величина угла возвышения равна алгебраической сумме угла прицеливания и угла места цели. Если цель выше горизонта, угол места цели имеет знак "+", если цель ниже горизонта, угол места цели имеет знак "-". | |||
| == Влияние сопротивления воздуха на траекторию полёта снаряда == | == Влияние сопротивления воздуха на траекторию полёта снаряда == | |||
| + | [[Файл:f95985fa3e89c016930ad47bdc5cca30.png|400 px|thumb|right|Рис. 5. Изменение траектории полёта снаряда от сопротивления воздуха]] | |||
| Траектория полёта снаряда в безвоздушном пространстве представляет собой симметричную кривую линию, называемую в математике параболой. Восходящая ветвь совпадает по форме с нисходящей ветвью и, следовательно, угол падения равен углу возвышения. | Траектория полёта снаряда в безвоздушном пространстве представляет собой симметричную кривую линию, называемую в математике параболой. Восходящая ветвь совпадает по форме с нисходящей ветвью и, следовательно, угол падения равен углу возвышения. | |||
| ? | + | |||
| ? | При полёте в воздухе снаряд расходует часть скорости на преодоление сопротивления воздуха. Таким образом, на снаряд в полёте действуют две силы — сила тяжести и сила сопротивления воздуха, которая уменьшает скорость и дальность полёта снаряда. Величина силы сопротивления воздуха зависит от формы снаряда, его размеров, скорости полёта и от плотности воздуха. Чем длиннее и заострённее головная часть снаряда, тем сопротивление воздуха меньше. Форма снаряда особенно сказывается при скоростях полёта, превышающих 330 метров в секунду (то есть при сверхзвуковых скоростях). | + | При полёте в воздухе снаряд расходует часть скорости на преодоление сопротивления воздуха. Таким образом, на снаряд в полёте действуют две силы — сила тяжести и сила сопротивления воздуха, которая уменьшает скорость и дальность полёта снаряда, как проиллюстрировано на рис. 5. Величина силы сопротивления воздуха зависит от формы снаряда, его размеров, скорости полёта и от плотности воздуха. Чем длиннее и заострённее головная часть снаряда, тем сопротивление воздуха меньше. Форма снаряда особенно сказывается при скоростях полёта, превышающих 330 метров в секунду (то есть при сверхзвуковых скоростях). | |
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca31.png|150 px|thumbnail|right|Недальнобойный и дальнобойный снаряды]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca31.png|150 px|thumbnail|right|Рис. 6. Недальнобойный и дальнобойный снаряды]] | |
| ? | На | + | На рис. 6 слева представлен недальнобойный снаряд старого образца и более продолговатый, заострённый дальнобойный снаряд справа. Также видно, что у дальнобойного снаряда в донной части делается коническое сужение. Дело в том, что сзади снаряда образуется разреженное пространство и завихрения, которые значительно увеличивают сопротивление воздуха. Сужением дна снаряда достигается уменьшение величины сопротивления воздуха, возникающего вследствие разреженности и завихрений за снарядом.<br /> | |
| Сила сопротивления воздуха пропорциональна скорости его полёта, но не прямо пропорциональна. Зависимость формализуется более сложно. Вследствие действия сопротивления воздуха у траектории полёта снаряда восходящая ветвь длиннее и отложе нисходящей. Угол падения больше угла возвышения.<br /> | Сила сопротивления воздуха пропорциональна скорости его полёта, но не прямо пропорциональна. Зависимость формализуется более сложно. Вследствие действия сопротивления воздуха у траектории полёта снаряда восходящая ветвь длиннее и отложе нисходящей. Угол падения больше угла возвышения.<br /> | |||
| ? | Помимо уменьшения дальности полёта снаряда и изменения формы траектории, сила сопротивления воздуха стремится опрокинуть снаряд, как это видно из | + | Помимо уменьшения дальности полёта снаряда и изменения формы траектории, сила сопротивления воздуха стремится опрокинуть снаряд, как это видно из рис. 7. | |
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca32.png|220 px|thumb|right|Силы, действующие на снаряд в полёте]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca32.png|220 px|thumb|right|Рис. 7. Силы, действующие на снаряд в полёте]] | |
| ? | Следовательно, невращающийся продолговатый снаряд под действием сопротивления воздуха будет переворачиваться. При этом снаряд может попасть в цель в любом положении, в том числе боком или дном, как показано на | + | Следовательно, невращающийся продолговатый снаряд под действием сопротивления воздуха будет переворачиваться. При этом снаряд может попасть в цель в любом положении, в том числе боком или дном, как показано на рис. 8. | |
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca33.png|300 px|thumb|right|Вращение снаряда в полёте под действием силы сопротивления воздуха]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca33.png|300 px|thumb|right|Рис. 8. Вращение снаряда в полёте под действием силы сопротивления воздуха]] | |
| Чтобы снаряд в полёте не переворачивался, ему придают вращательное движение с помощью нарезов в канале ствола.<br /> | Чтобы снаряд в полёте не переворачивался, ему придают вращательное движение с помощью нарезов в канале ствола.<br /> | |||
| ? | Если же рассмотреть воздействие воздуха на вращающийся снаряд, то можно увидеть, что это приводит к боковому отклонению траектории от плоскости стрельбы, как изображено на | + | Если же рассмотреть воздействие воздуха на вращающийся снаряд, то можно увидеть, что это приводит к боковому отклонению траектории от плоскости стрельбы, как изображено на рис. 9. | |
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca34.png|400 px|thumb|right|Деривация]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca34.png|400 px|thumb|right|Рис. 9. Деривация]] | |
| '''''Деривацией''''' называется отклонение снаряда от плоскости стрельбы вследствие его вращения. Если нарезы вьются слева вверх направо, то снаряд отклоняется вправо. | '''''Деривацией''''' называется отклонение снаряда от плоскости стрельбы вследствие его вращения. Если нарезы вьются слева вверх направо, то снаряд отклоняется вправо. | |||
| Строка 74: | Строка 76: | |||
| == Рассеивание снарядов == | == Рассеивание снарядов == | |||
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca35.png|300 px|thumb|right|Рассеивание снарядов]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca35.png|300 px|thumb|right|Рис. 10. Рассеивание снарядов]] | |
| ? | Если из одного и того же орудия, одинаковым боеприпасом, при одном и том же направлении ствола орудия, при одинаковых, на первый взгляд, условиях произвести несколько выстрелов, то снаряды не попадут в одну точку, а полетят по разным траекториям, образуя пучок траекторий. Это явление называется '''''рассеиванием снарядов'''''. | + | Если из одного и того же орудия, одинаковым боеприпасом, при одном и том же направлении ствола орудия, при одинаковых, на первый взгляд, условиях произвести несколько выстрелов, то снаряды не попадут в одну точку, а полетят по разным траекториям, образуя пучок траекторий, как проиллюстрировано на рис. 10. Это явление называется '''''рассеиванием снарядов'''''. | |
| ? | + | |||
| ? | Причиной рассеивания снарядов является невозможность достижения абсолютно одинаковых условий для каждого выстрела. В таблице | + | Причиной рассеивания снарядов является невозможность достижения абсолютно одинаковых условий для каждого выстрела. В таблице приведены основные факторы, вызывающие рассеивание снарядов и возможные пути уменьшения этого рассеивания. | |
| + | {| class="wikitable" | |||
| + | |- | |||
| + | ! Основные группы причин рассеивания !! Условия, порождающие причины рассеивания !! Меры борьбы за уменьшение рассеивания | |||
| + | |- | |||
| + | | 1. Разнообразие начальных скоростей | |||
| + | || | |||
| + | * Разнообразие свойств пороха (состав, содержание влаги и растворителя). | |||
| + | * Разнообразие веса зарядов. | |||
| + | * Разнообразие температуры зарядов. | |||
| + | * Разнообразие плотности заряжания. | |||
| + | (размеры и расположение ведущего пояска, досылка снарядов). | |||
| + | * Разнообразие формы и веса снарядов. | |||
| + | || | |||
| + | * Хранение в герметической укупорке. Каждую стрельбу производить зарядами одной партии. | |||
| + | * Поддержание должной температуры в погребе. | |||
| + | * Единообразие заряжания. | |||
| + | * Каждую стрельбу производить снарядами одного весового знака. | |||
| + | |- | |||
| + | | 2. Разнообразие углов бросания | |||
| + | || | |||
| + | * Разнообразие углов возвышения (мёртвые ходы в прицельном устройстве и в механизме вертикального наведения). | |||
| + | * Разнообразие углов вылета. | |||
| + | * Разнообразие наводки. | |||
| + | || | |||
| + | * Тщательный уход за материальной частью. | |||
| + | * Хорошая тренировка наводчиков. | |||
| + | |- | |||
| + | | 3. Разнообразие условий в полёте снаряда | |||
| + | || | |||
| + | Разнообразие влияния воздушной среды (плотность, ветер). | |||
| + | || | |||
| + | - | |||
| + | |} | |||
| Площадь, на которую падают снаряды, выпущенные из орудия при одном и том же направлении канала ствола, называется '''''площадью рассеивания'''''.<br /> | Площадь, на которую падают снаряды, выпущенные из орудия при одном и том же направлении канала ствола, называется '''''площадью рассеивания'''''.<br /> | |||
| Строка 89: | Строка 124: | |||
| Интенсивность, с которой снаряды попадают в различные точки эллипса рассеивания, описывается двумерным Гауссовским (нормальным) законом распределения. Отсюда, если следовать в точности законам теории вероятностей, можно сделать вывод, что эллипс рассеивания является идеализацией. Процент попаданий снарядов внутрь эллипса описывается правилом трёх сигма, а именно, вероятность попадания снарядов в эллипс, величина оси которого равна утроенному квадратному корню из дисперсий соответствующих одномерных Гауссовских законов распределения равна 0.9973.<br /> | Интенсивность, с которой снаряды попадают в различные точки эллипса рассеивания, описывается двумерным Гауссовским (нормальным) законом распределения. Отсюда, если следовать в точности законам теории вероятностей, можно сделать вывод, что эллипс рассеивания является идеализацией. Процент попаданий снарядов внутрь эллипса описывается правилом трёх сигма, а именно, вероятность попадания снарядов в эллипс, величина оси которого равна утроенному квадратному корню из дисперсий соответствующих одномерных Гауссовских законов распределения равна 0.9973.<br /> | |||
| В силу того, что количество выстрелов из одного орудия, особенно крупного калибра, как уже было указано выше, в силу износа зачастую не превышает и одной тысячи, этой неточностью можно пренебречь и считать, что все снаряды попадают в эллипс рассеивания. Любое сечение пучка траекторий полёта снарядов также представляет собой эллипс. Рассеивание снарядов по дальности всегда больше, чем в боковом направлении и по высоте. Величину срединных отклонений можно найти в основной таблице стрельбы и по ней определить размеры эллипса.<br /> | В силу того, что количество выстрелов из одного орудия, особенно крупного калибра, как уже было указано выше, в силу износа зачастую не превышает и одной тысячи, этой неточностью можно пренебречь и считать, что все снаряды попадают в эллипс рассеивания. Любое сечение пучка траекторий полёта снарядов также представляет собой эллипс. Рассеивание снарядов по дальности всегда больше, чем в боковом направлении и по высоте. Величину срединных отклонений можно найти в основной таблице стрельбы и по ней определить размеры эллипса.<br /> | |||
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca37.png|300 px|thumb|right|Стрельба по цели, не имеющей глубины]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca37.png|300 px|thumb|right|Рис. 11. Стрельба по цели, не имеющей глубины]] | |
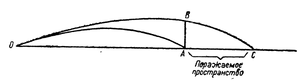
| '''''Поражаемым пространством''''' называется пространство, на протяжении которого траектория проходит через цель. | '''''Поражаемым пространством''''' называется пространство, на протяжении которого траектория проходит через цель. | |||
| ? | Согласно | + | Согласно рис. 11, поражаемое пространство равно расстоянию по горизонту АС от основания цели до конца траектории, проходящей через вершину цели. Каждый снаряд, упавший вне поражаемого пространства, прошёл либо выше цели, либо упал до неё. Поражаемое пространство ограничивается двумя траекториями — траекторией ОА, проходящей через основание цели, и траекторией ОС, проходящей через верхнюю точку цели. <br /> | |
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca38.png|300 px|thumb|right|Стрельба по цели, имеющей глубину]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca38.png|300 px|thumb|right|Рис. 12. Стрельба по цели, имеющей глубину]] | |
| ? | В случае, если поражаемая цель имеет глубину, величина поражаемого пространства увеличивается на величину глубины цели. | + | В случае, если поражаемая цель имеет глубину, величина поражаемого пространства увеличивается на величину глубины цели, как проиллюстрировано на рис. 12. | |
| Глубина цели будет зависеть от размеров цели и её положения относительно плоскости стрельбы. Рассмотрим цель, наиболее вероятную для морской артиллерии — судно неприятеля. В таком случае, если цель идёт от нас или на нас, глубина цели равна её длине, когда цель идёт перпендикулярно к плоскости стрельбы, глубина равна ширине цели, как проиллюстрировано на рисунке. | Глубина цели будет зависеть от размеров цели и её положения относительно плоскости стрельбы. Рассмотрим цель, наиболее вероятную для морской артиллерии — судно неприятеля. В таком случае, если цель идёт от нас или на нас, глубина цели равна её длине, когда цель идёт перпендикулярно к плоскости стрельбы, глубина равна ширине цели, как проиллюстрировано на рисунке. | |||
| Учитывая тот факт, что эллипс рассеивания имеет большую длину и малую ширину, можно сделать вывод о том, что при малой глубине цели снарядов в цель попадает меньше, чем при большой её глубине. То есть, чем больше глубина цели, тем легче в неё попасть. С увеличением дальности стрельбы поражаемое пространство цели уменьшается, так как увеличивается угол падения.<br /> | Учитывая тот факт, что эллипс рассеивания имеет большую длину и малую ширину, можно сделать вывод о том, что при малой глубине цели снарядов в цель попадает меньше, чем при большой её глубине. То есть, чем больше глубина цели, тем легче в неё попасть. С увеличением дальности стрельбы поражаемое пространство цели уменьшается, так как увеличивается угол падения.<br /> | |||
| ? | '''''Прямым выстрелом''''' называется выстрел, при котором всё расстояние от точки вылета до точки падения является поражаемым пространством. | + | '''''Прямым выстрелом''''' называется выстрел, при котором всё расстояние от точки вылета до точки падения является поражаемым пространством (см. рис. 13). | |
| ? | [[Файл:f95985fa3e89c016930ad47bdc5cca40.png|300 px|thumb|right|Прямой выстрел]] | + | [[Файл:f95985fa3e89c016930ad47bdc5cca40.png|300 px|thumb|right|Рис. 13. Прямой выстрел]] | |
| Это получается в том случае, если высота траектории не превышает высоту цели. Дальность прямого выстрела зависит от крутизны траектории и высоты цели.<br /> | Это получается в том случае, если высота траектории не превышает высоту цели. Дальность прямого выстрела зависит от крутизны траектории и высоты цели.<br /> | |||
Версия 07:20, 2 ноября 2014
Содержание
Основные понятия
Точкой вылета называется центр дульного среза орудия.
Точкой падения называется точка пересечения траектории с горизонтом орудия.
Горизонтом орудия называется горизонтальная плоскость, проходящая через точку вылета.
Линией возвышения называется продолжение оси канала ствола наведённого орудия.
Линией бросания ОВ называется продолжение оси канала ствола в момент выстрела. В момент выстрела орудие вздрагивает, вследствие чего снаряд бросается не по линии возвышения ОА, а по линии бросания ОВ (см. рис. 2).
Линией цели ОЦ называется линия, соединяющая орудие с целью (см. рис. 2).
Линией прицеливания (визирования) называется линия, идущая от глаза наводчика через оптическую ось прицела в точку наводки. При стрельбе прямой наводкой, когда линия прицеливания направлена в цель, линия прицеливания совпадает с линией цели.
Линией падения называется касательная к траектории в точке падения.
Углом возвышения (греческая фи) называется угол между линией возвышения и горизонтом орудия. Если ось канала ствола направлена ниже горизонта, то этот угол называется углом снижения (см. рис. 2).
Углом бросания (греческая тета ноль) называется угол между линией бросания и горизонтом орудия (см. рис. 2).
Углом вылета (греческая гамма) называется угол между линией бросания и линией возвышения. В морской артиллерии угол вылета имеет малую величину и его иногда в расчёт не принимают, полагая, что снаряд бросается под углом возвышения (см. рис. 2).
Углом прицеливания (греческая альфа) называется угол между линией возвышения и линией прицеливания (см. рис. 2).
Углом места цели (греческая эпсилон) называется угол между линией цели и горизонтом орудия. При стрельбе корабля по морским целям угол места цели равен нулю, так как линия цели направлена по горизонту орудия (см. рис. 2).
Углом падения (греческая тета с латинской буквой с) называется угол между линией цели и линией падения (см. рис. 2).
Углом встречи (греческая мю) называется угол между линией падения и касательной к поверхности цели в точке встречи (см. рис. 2).
Плоскостью стрельбы называется вертикальная плоскость, проходящая через линию возвышения. При стрельбе корабля по морским целям линия прицеливания направлена по горизонту, в этом случае угол возвышения равен углу прицеливания. При стрельбе корабля по береговым и воздушным целям угол возвышения равен сумме угла прицеливания и угла места цели (см. рис. 3). При стрельбе береговой батареи по морским целям угол возвышения равен разности угла прицеливания и угла места цели (см. рис. 4). Таким образом, величина угла возвышения равна алгебраической сумме угла прицеливания и угла места цели. Если цель выше горизонта, угол места цели имеет знак "+", если цель ниже горизонта, угол места цели имеет знак "-".
Влияние сопротивления воздуха на траекторию полёта снаряда
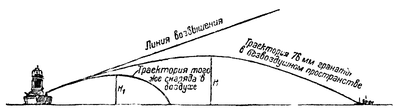
Траектория полёта снаряда в безвоздушном пространстве представляет собой симметричную кривую линию, называемую в математике параболой. Восходящая ветвь совпадает по форме с нисходящей ветвью и, следовательно, угол падения равен углу возвышения.
При полёте в воздухе снаряд расходует часть скорости на преодоление сопротивления воздуха. Таким образом, на снаряд в полёте действуют две силы — сила тяжести и сила сопротивления воздуха, которая уменьшает скорость и дальность полёта снаряда, как проиллюстрировано на рис. 5. Величина силы сопротивления воздуха зависит от формы снаряда, его размеров, скорости полёта и от плотности воздуха. Чем длиннее и заострённее головная часть снаряда, тем сопротивление воздуха меньше. Форма снаряда особенно сказывается при скоростях полёта, превышающих 330 метров в секунду (то есть при сверхзвуковых скоростях).
На рис. 6 слева представлен недальнобойный снаряд старого образца и более продолговатый, заострённый дальнобойный снаряд справа. Также видно, что у дальнобойного снаряда в донной части делается коническое сужение. Дело в том, что сзади снаряда образуется разреженное пространство и завихрения, которые значительно увеличивают сопротивление воздуха. Сужением дна снаряда достигается уменьшение величины сопротивления воздуха, возникающего вследствие разреженности и завихрений за снарядом.
Сила сопротивления воздуха пропорциональна скорости его полёта, но не прямо пропорциональна. Зависимость формализуется более сложно. Вследствие действия сопротивления воздуха у траектории полёта снаряда восходящая ветвь длиннее и отложе нисходящей. Угол падения больше угла возвышения.
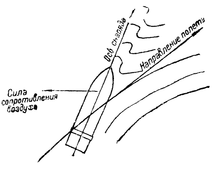
Помимо уменьшения дальности полёта снаряда и изменения формы траектории, сила сопротивления воздуха стремится опрокинуть снаряд, как это видно из рис. 7.
Следовательно, невращающийся продолговатый снаряд под действием сопротивления воздуха будет переворачиваться. При этом снаряд может попасть в цель в любом положении, в том числе боком или дном, как показано на рис. 8.
Чтобы снаряд в полёте не переворачивался, ему придают вращательное движение с помощью нарезов в канале ствола.
Если же рассмотреть воздействие воздуха на вращающийся снаряд, то можно увидеть, что это приводит к боковому отклонению траектории от плоскости стрельбы, как изображено на рис. 9.
Деривацией называется отклонение снаряда от плоскости стрельбы вследствие его вращения. Если нарезы вьются слева вверх направо, то снаряд отклоняется вправо.
Влияние угла возвышения и начальной скорости снаряда на дальность его полёта
Дальность полёта снаряда зависит от углов возвышения, под которыми он бросается. Увеличение дальности полёта с увеличением угла возвышения происходит только до некоторого предела (40-50 градусов), при дальнейшем увеличении угла возвышения, дальность начинает уменьшаться.
Углом предельной дальности называется угол возвышения, при котором получается наибольшая дальность стрельбы при данной начальной скорости и снаряде.
При стрельбе в безвоздушном пространстве наибольшая дальность полёта снаряда получается при угле возвышения 45 градусов. При стрельбе в воздухе величина угла предельной дальности отличается от этого значения и у разных орудий бывает неодинаковой (обычно меньше 45 градусов). Для сверхдальнобойной артиллерии, когда снаряд значительную часть пути летит на большой высоте в сильно разреженном воздухе, угол предельной дальности бывает более 45 градусов.
Для орудия данного образца и при стрельбе определенным типом боеприпаса каждому углу возвышения соответствует строго определенная дальность полёта снаряда. Следовательно, чтобы забросить снаряд на нужное нам расстояние, необходимо орудию придать угол возвышения, соответствующий этому расстоянию.
Траектории снарядов, выпущенных при углах возвышения меньших, чем угол предельной дальности, называются настильными траекториями.
Траектории снарядов, выпущенных при углах возвышения меньших, чем угол предельной дальности, называются 'навесными траекториями'.
Рассеивание снарядов
Если из одного и того же орудия, одинаковым боеприпасом, при одном и том же направлении ствола орудия, при одинаковых, на первый взгляд, условиях произвести несколько выстрелов, то снаряды не попадут в одну точку, а полетят по разным траекториям, образуя пучок траекторий, как проиллюстрировано на рис. 10. Это явление называется рассеиванием снарядов.
Причиной рассеивания снарядов является невозможность достижения абсолютно одинаковых условий для каждого выстрела. В таблице приведены основные факторы, вызывающие рассеивание снарядов и возможные пути уменьшения этого рассеивания.
| Основные группы причин рассеивания | Условия, порождающие причины рассеивания | Меры борьбы за уменьшение рассеивания |
|---|---|---|
| 1. Разнообразие начальных скоростей |
(размеры и расположение ведущего пояска, досылка снарядов).
|
|
| 2. Разнообразие углов бросания |
|
|
| 3. Разнообразие условий в полёте снаряда |
Разнообразие влияния воздушной среды (плотность, ветер). |
- |
Площадь, на которую падают снаряды, выпущенные из орудия при одном и том же направлении канала ствола, называется площадью рассеивания.
Середина площади рассеивания называется средней точкой падения.
Воображаемая траектория, проходящая через точку вылета и среднюю точку падения, называется средней траекторией.
Площадь рассеивания имеет форму эллипса, поэтому площадь рассеивания называется эллипсом рассеивания.
Интенсивность, с которой снаряды попадают в различные точки эллипса рассеивания, описывается двумерным Гауссовским (нормальным) законом распределения. Отсюда, если следовать в точности законам теории вероятностей, можно сделать вывод, что эллипс рассеивания является идеализацией. Процент попаданий снарядов внутрь эллипса описывается правилом трёх сигма, а именно, вероятность попадания снарядов в эллипс, величина оси которого равна утроенному квадратному корню из дисперсий соответствующих одномерных Гауссовских законов распределения равна 0.9973.
В силу того, что количество выстрелов из одного орудия, особенно крупного калибра, как уже было указано выше, в силу износа зачастую не превышает и одной тысячи, этой неточностью можно пренебречь и считать, что все снаряды попадают в эллипс рассеивания. Любое сечение пучка траекторий полёта снарядов также представляет собой эллипс. Рассеивание снарядов по дальности всегда больше, чем в боковом направлении и по высоте. Величину срединных отклонений можно найти в основной таблице стрельбы и по ней определить размеры эллипса.
Поражаемым пространством называется пространство, на протяжении которого траектория проходит через цель.
Согласно рис. 11, поражаемое пространство равно расстоянию по горизонту АС от основания цели до конца траектории, проходящей через вершину цели. Каждый снаряд, упавший вне поражаемого пространства, прошёл либо выше цели, либо упал до неё. Поражаемое пространство ограничивается двумя траекториями — траекторией ОА, проходящей через основание цели, и траекторией ОС, проходящей через верхнюю точку цели.
В случае, если поражаемая цель имеет глубину, величина поражаемого пространства увеличивается на величину глубины цели, как проиллюстрировано на рис. 12. Глубина цели будет зависеть от размеров цели и её положения относительно плоскости стрельбы. Рассмотрим цель, наиболее вероятную для морской артиллерии — судно неприятеля. В таком случае, если цель идёт от нас или на нас, глубина цели равна её длине, когда цель идёт перпендикулярно к плоскости стрельбы, глубина равна ширине цели, как проиллюстрировано на рисунке.
Учитывая тот факт, что эллипс рассеивания имеет большую длину и малую ширину, можно сделать вывод о том, что при малой глубине цели снарядов в цель попадает меньше, чем при большой её глубине. То есть, чем больше глубина цели, тем легче в неё попасть. С увеличением дальности стрельбы поражаемое пространство цели уменьшается, так как увеличивается угол падения.
Прямым выстрелом называется выстрел, при котором всё расстояние от точки вылета до точки падения является поражаемым пространством (см. рис. 13).
Это получается в том случае, если высота траектории не превышает высоту цели. Дальность прямого выстрела зависит от крутизны траектории и высоты цели.
Дальностью прямого выстрела (или дальностью настильности) называется расстояние, на котором высота траектории не превышает высоты цели.
Ссылки
https://ru.wikipedia.org/wiki/корабельная_артиллерия
Литература
- Гончаров Л. Г. Курс морской тактики артиллерия и броня. Ленинград: Издательство Военно-Морской Академии РККА им. тов. Ворошилова. 1932. 390 с.
- Травиничев А. Корабельная артиллерия. М.: Государственное военно-морское издательство НКВМФ союза ССР. 1941. 135 с.
- Мордашев Ю. Н., Абрамович И. Е., Меккель М. А. Учебник комендора палубной артиллерии. М.: Военное издательство Министерства вооружённых сил союза ССР. 1947. 176 с.