Локсодромия
| Версия 10:49, 14 марта 2015 | Версия 10:50, 14 марта 2015 | |||
| Строка 1: | Строка 1: | |||
| ? | + | '''Локсодромия''' (от греч. loxós — косой и drómos — бег, путь), линия на сфере или какой-либо другой поверхности вращения, пересекающая все меридианы под постоянным углом. <br /> | ||
| ? | + | |||
| ? | + | |||
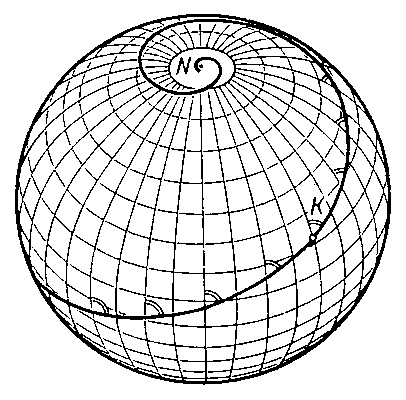
| [[Файл:Локсодромия_на_сфере.gif|framed| Локсодромия на сфере, пересекающая все меридианы под углом К = 70°.]] | [[Файл:Локсодромия_на_сфере.gif|framed| Локсодромия на сфере, пересекающая все меридианы под углом К = 70°.]] | |||
| Локсодромия и [[Ортодромия]] на сфере введены и изучены в 1624 В. Снеллиусом. На сфере и сжатом эллипсоиде вращения при К = 0° и К = 180° Локсодромия совпадает с меридианом, при К = ±90° — с географической параллелью; в др. случаях локсодромия имеет вид спирали: делая бесконечное множество витков по поверхности, неограниченно приближается к её полюсам. На картах в Меркатора проекции все локсодромии изображаются прямыми линиями. Локсодромия широко используется в [[Навигация|морской навигации]] и в аэронавигации, где угол К трактуется как истинный курс корабля или самолёта. Применение локсодромии вместо [[ортодромии]], представляющей кратчайшее расстояние между двумя точками сферы, вызвано практическими удобствами управления судном или самолётом, хотя в этом случае путь оказывается длиннее. При К ≠ 0° (или 180°) разность длин локсодромии и [[ортодромии]], соединяющих две заданные точки, пропорциональна расстоянию между этими точками и удалению от экватора. Локсодромия иногда используют в [[Сфероидическая геодезия|сфероидической геодезии]]. Широким обобщением локсодромия являются Изогональные траектории заданного семейства кривых на произвольных поверхностях. | Локсодромия и [[Ортодромия]] на сфере введены и изучены в 1624 В. Снеллиусом. На сфере и сжатом эллипсоиде вращения при К = 0° и К = 180° Локсодромия совпадает с меридианом, при К = ±90° — с географической параллелью; в др. случаях локсодромия имеет вид спирали: делая бесконечное множество витков по поверхности, неограниченно приближается к её полюсам. На картах в Меркатора проекции все локсодромии изображаются прямыми линиями. Локсодромия широко используется в [[Навигация|морской навигации]] и в аэронавигации, где угол К трактуется как истинный курс корабля или самолёта. Применение локсодромии вместо [[ортодромии]], представляющей кратчайшее расстояние между двумя точками сферы, вызвано практическими удобствами управления судном или самолётом, хотя в этом случае путь оказывается длиннее. При К ≠ 0° (или 180°) разность длин локсодромии и [[ортодромии]], соединяющих две заданные точки, пропорциональна расстоянию между этими точками и удалению от экватора. Локсодромия иногда используют в [[Сфероидическая геодезия|сфероидической геодезии]]. Широким обобщением локсодромия являются Изогональные траектории заданного семейства кривых на произвольных поверхностях. | |||
Версия 10:50, 14 марта 2015
Локсодромия (от греч. loxós — косой и drómos — бег, путь), линия на сфере или какой-либо другой поверхности вращения, пересекающая все меридианы под постоянным углом.
Локсодромия и Ортодромия на сфере введены и изучены в 1624 В. Снеллиусом. На сфере и сжатом эллипсоиде вращения при К = 0° и К = 180° Локсодромия совпадает с меридианом, при К = ±90° — с географической параллелью; в др. случаях локсодромия имеет вид спирали: делая бесконечное множество витков по поверхности, неограниченно приближается к её полюсам. На картах в Меркатора проекции все локсодромии изображаются прямыми линиями. Локсодромия широко используется в морской навигации и в аэронавигации, где угол К трактуется как истинный курс корабля или самолёта. Применение локсодромии вместо ортодромии, представляющей кратчайшее расстояние между двумя точками сферы, вызвано практическими удобствами управления судном или самолётом, хотя в этом случае путь оказывается длиннее. При К ≠ 0° (или 180°) разность длин локсодромии и ортодромии, соединяющих две заданные точки, пропорциональна расстоянию между этими точками и удалению от экватора. Локсодромия иногда используют в сфероидической геодезии. Широким обобщением локсодромия являются Изогональные траектории заданного семейства кривых на произвольных поверхностях.
Лит.: Каврайский В. В., Избр. труды, т. 2, в. 2, [М.], 1959. Г. А. Мещеряков.