Строгая теория серий сливов и эксперимент

Теория серий сливов

Это небольшое исследование поможет понять, откуда на самом деле берутся серии поражений и насколько часто они могут возникать. Лично мне успешное решение этого вопроса позволяет сохранять хорошее настроение вне зависимости от результатов боёв за вечер. Возможно, оно поможет и вам. Автор статьи: Med433

Тема о сериях поражений является, пожалуй, одной из самых популярных на танковых форумах. Десяток сливов, идущих подряд, могут не слабо подпортить настроение. Порой закрадывается мысль, что случайностью это быть не может, ВБР сегодня настроен по-особому и специально кидает к слабым союзникам. Игрок идёт на форум и создаёт тему в духе «НАКИПЕЛО!!1». Поскольку ситуация знакома каждому, всегда найдутся сочувствующие, которые подтвердят наличие заговора, а также и тролли, которые посоветуют выровнять руки.

Запрограммирован ли балансировщик раз за разом кидать игрока к слабым союзникам? Является ли результат каждого боя случайным, или же существуют скрытые механизмы, удлиняющие серии поражений у злостных неплательщиков? Можно долго и усердно, с пеной у рта доказывать свою точку зрения, это весьма занятное дело и форум буквально завален такими публикациями. Однако возможен и другой очевидный, хоть и трудный, путь – записать результаты множества боёв, посчитать число серий и сравнить с расчётами для «честного» ВБРа. Вот этим я и занимался последние тысячу с хвостиком боёв. Поскольку хватать карандаш и блокнот после каждого боя быстро надоедает, я наваял небольшую программку, которая записывает историю боёв автоматически в такой файл (21 КБ).

Первое, что необходимо проверить – это независимость результата боя от исхода предыдущих боёв. Если в последнем бою я победил, то в следующем шансы на победу будут выше? Я ведь сегодня на коне и зверски тащу? А если я проиграл, значит, я сегодня лажаю, и в следующем бою тоже скорее всего потерплю поражение? Или, может, наоборот, после поражения я напрягусь, и постараюсь всеми способами победить, зарядив полный комплект кумулятивов? Наличие длинной цепочки результатов позволяет однозначно ответить на этот вопрос.

Рассмотрим, для примера, первые несколько боёв из этой цепочки результатов (1 - победа, 0 - поражение):

000100101011111110...

Красным цветом выделены бои, которым предшествовало поражение, а перед зелёными была победа. Нужно сравнить процент побед для «зелёных» и для «красных» боёв. Кропотливо обработав всю цепочку, получим такой результат: процент побед «после победы» равен 57.14 а после поражения – 57.78. Значения оказались очень близки, для цепочки такой длины – 1269 боёв – расхождение меньше статистического отклонения. Иными словами, процент побед для зелёных и красных боёв одинаков.

Таким образом, мы пришли к выводу, для некоторых очевидному и ожидаемому, для других – парадоксальному: вероятность победы никак не зависит от результата предыдущего боя. Благодаря этому свойству, мы можем применить простейшую теорию вероятности для анализа цепочки. Изначально меня интересовало, насколько часто встречаются серии поражений различной длины.

Теория

Пусть вероятность победы p. Нас интересует, как часто встречаются серии из n поражений подряд. Обозначим за W_n среднее число серий из n поражений, поделённое на число боёв. Как найти зависимость Wn от n и p? Лично я получил ответ экспериментально, после долгой возни с генератором случайных чисел, но когда ответ уже известен, легко указать элегантное решение.

Первое, что нужно сделать – это обосновать равенство

W_n+1=(1-n)*W_n.

Это значит, что серия из n+1 поражений встречается реже серии из n поражений ровно в (1-p) раз. Кому интересно, можете поупражняться в доказательстве. Из этого следует вывод, что

W_n=const*(1-p)ⁿ

Осталось лишь найти постоянный множитель. В сумме по n произведения n*W_n должны дать процент поражений. Итого, имеем

W_n=p²(1-p)ⁿ.

Для сравнения с экспериментом и интуитивного понимания полезно рассчитать следующие величины.

1. Как часто встречается серия из n поражений.

В среднем, раз в 1/W_n боёв.

2. Сколько серий из n поражений в среднем должно получиться в экперименте. Приблизительно, N*W_n, где N – длина цепочки.

Майндфаки для ценителей (ну вдруг такие найдутся)

1. Формула для плотности n поражений W_n=p²(1-p)ⁿ. Для такой же серий побед надо заменить р на 1-р. Любопытно, что для n=2 плотность побед равна плотности поражений. Иными словами, пара побед встречается также часто, как и пара поражений. Внезависимости от мастерства: хоть у бота на КВ-5, хоть у адского нагибатора на Минимаусе. Придумать этому красивое объяснение.
2. Чему соответствует значение W₀? Что такое серия из нуля поражений?
3. Посчитать дисперсию W_n аналитически.

В таблице «теоретическая оценка ошибки» – результат численной симуляции

А на практике...

...нужно просто посчитать число серий в цепочке результатов. Для начала пример. В данном кусочке

000100101011111110...

3 серии из одного поражения, одна - из двух и одна - из трёх. Для всей же цепочки результат приведён в таблице:

длина серии n	1	2	3	4	5	6	7	8	9	10	11	12
количество серий в эксперименте	184	73	31	14	7	3	0	0	1	0	0	0
теоретическое количество N p2(1-p)n таких серий, N=1269, p=0.574	178	76	32	14	6	2,5	1,1	0,45	0,19	0,08	0,03	0,02
теоретическая оценка ошибки	12	8	5	3,5	2,4	1,6	1	0,7	0,4	0,3	0,2	0,1
теоретическая частота возникновения такой серии	7	17	39	92	216	506	1187	2785	6532	15322	35939	84301

Первая строка - длина серии (одно поражение между двумя победами - это серия длиной 1 :) ). Далее следуют число серий, подсчитанное в цепочке и теоретическое предсказание этой величины. В самой длинной серии набралось 9 поражений подряд. Теоретическая оценка ошибки - оценка ожидаемого расхождения между экспериментом и теорией, возникающее из-за не бесконечной длины цепочки. Последняя строка - теоретическая частота возникновения серии. К примеру, серия из 12 поражений должна встречаться в среднем раз в 84301 бой. Для полноты картины тоже самое проделано для серий побед:

длина серии	1	2	3	4	5	6	7	8	9	10	11	12
количество серий в эксперименте	136	79	31	34	15	5	5	2	3	0	2	0
теоретическое количество N(1-p)2pn таких серий, N=1269, p=0.574	132	76	44	25	14	8	5	2,7	1,5	0,9	0,5	0,3
теоретическая оценка ошибки	11	8	6	5	4	3	2	1,6	1,2	0,9	0,7	0,5
теоретическая частота возникновения такой серии	10	17	29	51	89	154	269	469	818	1425	2484	4330

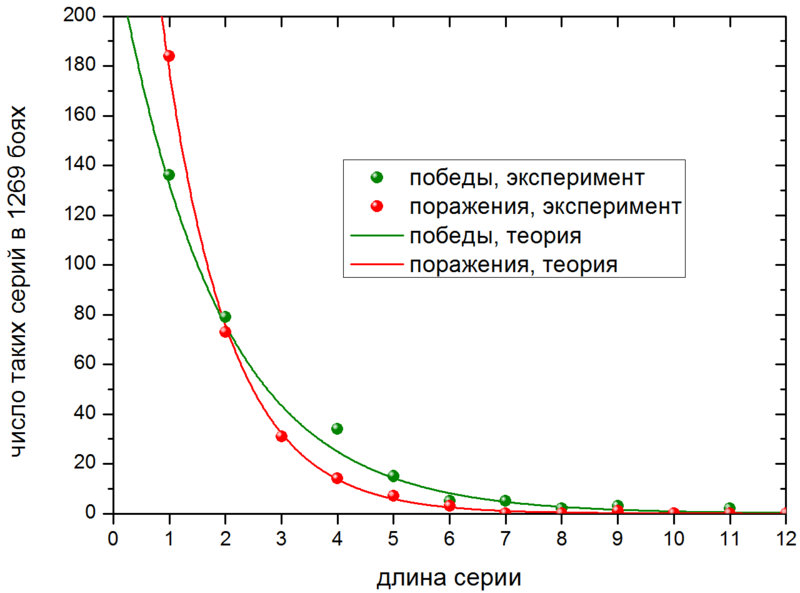
Ну и всеобщая картина маслом:

И что тут таки нарисовано?

Сравнение теории с экспериментом приводит к следующим выводам. Простейшая теория вероятностей вполне сносно предсказывает число серий побед и поражений в достаточно длинной цепочке боёв. Для этого нужно знать лишь процент побед игрока и общее число боёв. В моём случае процент побед выше пятидесяти, и серии побед встречаются чаще, чем серии поражений, в полном соответствии с теорией.

Должен признаться, что такая картина совершенно противоречит ощущениям от игры. Я прекрасно помню длинные серии поражений и не припоминаю эпических серий побед. Психология оказывается забавной штукой. Уже после четырёх-пяти поражений к ряду ко мне начинает закрадываться чувство вселенской несправедливости. Напротив, серии из одиннадцати побед я скорее всего и не заметил бы, если бы специально не записывал результаты. Серии побед воспринимаются как нечто само собой разумеющееся и совершенно не откладываются в памяти.

Подводя итог, еще раз озвучу главную мысль - ответ на вопрос, откуда берутся серии сливов. Как ни банально это звучит, но время от времени несколько поражений происходят подряд просто в силу случайности. Средняя частота таких серий определяется процентом побед игрока и может быть вычислена математически по его проценту побед. В силу особенностей восприятия может возникнуть впечатление тотального превосходства серий поражений над сериями побед, однако при проверке обнаруживается, что это лишь иллюзия.

Ссылки

• Обсуждение статьи на официальном форуме World of Tanks